

Transverse internal area can be expressed asĪ a = transverse internal area (in 2) Circumference ExternalĮxternal circumference can be expressed asĬ e = external circumference (in) Circumference Internal Internal pipe or tube surface per ft of length can be expressed asĪ i = internal pipe surface area (ft 2 per ft pipe) Transverse Internal Area
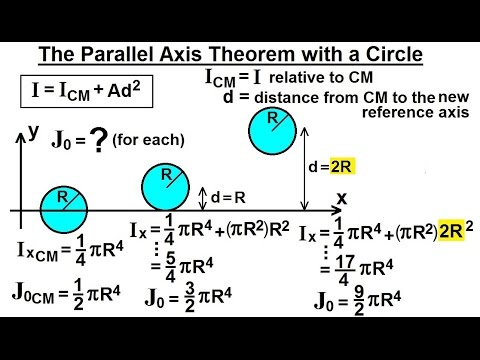
Transverse metal area can be expressed asĪ m = transverse metal area (in 2) External Pipe SurfaceĮxternal pipe or tube surface per ft of length can be expressed asĪ o = external pipe surface area (ft 2 per ft pipe) Internal Pipe Surface Section modulus is a geometric property for a given cross-section used in the design of beams or flexural members. The calculator is based on the piping formulas and equations below.ĭ i = inside diameter (in) Section Modulus Make Shortcut to this Calculator on Your Home Screen?.Integrating curvatures over beam length, the deflection, at some point along x-axis, should also be reversely proportional to I.Inside diameter (in) - (default values: STD 4 inches - Carbon, Alloy and Stainless Steel Pipes - ASME/ANSI B36.10/19 Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. Therefore, the definite integral for the moment of inertia of the circle should be written as: To do so, we consider for the arbitrary point P (see figure) the blue colored right triangle and using simple trigonometry we find: y=r \sin\varphi Moreover, the coordinate y of any point, can be expressed in terms of the polar coordinates r and φ. With this coordinate system, the differential area dA now becomes: dA=dr\: ds = dr \:(rd\varphi)=r\:dr \:d\varphi, where ds is the differential arc length for differential angle dφ.įurthermore, the area, enclosed by the circle, should have these boundaries: Specifically, for any point of the plane, r is the distance from pole and φ is the angle from the polar axis L, measured in counter-clockwise direction. Instead we choose a polar system, with its pole O coinciding with circle center, and its polar axis L coinciding with the axis of rotation x, as depicted in the figure below. Since we have a circular area, the Cartesian x,y system is not the best option. First we must define the coordinate system. Using the above definition, which applies for any closed shape, we will try to reach to the final equation for the moment of inertia of circle, around an axis x passing through its center. Depending on the context, an axis passing through the center may be implied, however, for more complex shapes it is not guaranteed that the implied axis would be obvious.įrom the definition also, it is also apparent that the moment of inertia should always have a positive value, since there is only a squared term inside the integral.įinding the equation for the moment of inertia of a circle Often though, one may use the term "moment of inertia of circle", missing to specify an axis. Where A is the area of the shape and y the distance of any point inside area A from a given axis of rotation.įrom this definition it becomes clear that the moment of inertia is not a property of the shape alone but is always related to an axis of rotation.
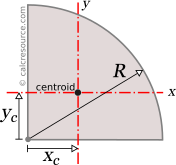
The second moment of area of any planar, closed shape is given by the following integral: Typical units for the moment of inertia, in metric, are: Typical units for the moment of inertia, in the imperial system of measurements are:
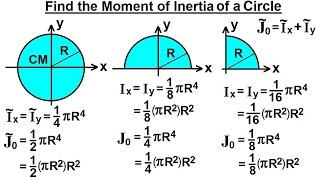
By definition, the moment of inertia is the second moment of area, in other words the integral sum of cross-sectional area times the square distance from the axis of rotation, hence its dimensions are ^4. In fact, this is true for the moment of inertia of any shape, not just the circle. Since those are lengths, one can expect that the units of moment of inertia should be of the type: ^4. The above equations for the moment of inertia of circle, reveal that the latter is analogous to the fourth power of circle radius or diameter. The moment of inertia of circle with respect to any axis passing through its centre, is given by the following expression:Įxpressed in terms of the circle diameter D, the above equation is equivalent to:


 0 kommentar(er)
0 kommentar(er)
